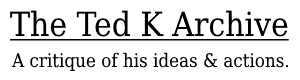The Great Leap Forward: Anatomy of a Central Planning Disaster

We are grateful to Mark An, who as a coauthor of earlier versions provided invaluable inputs for this research. We would also like to thank Rich Ashley, Dwayne Benjamin, Loren Brandt, Gregory Chow, Belton Fleisher, Roger Gordon, Ted Groves, Steven Haider, Allen Kelley, Steven Levitt (the editor), Barry Naughton, Yingyi Qian, Jim Rauch, Gerard Roland, Djavad Salehi, James Wen, Yaohui Zhao, Xiaodong Zhu, two anonymous referees, and seminar participants at Duke University, Michigan State University, North Carolina State University, Peking University, University of California at Berkeley, University of California at San Diego, University of Chicago, University of Toronto, University of Virginia, and Virginia Polytechnic Institute and State University for constructive suggestions and comments. We are also grateful to Xian Zude, Sheng Laiyun, Wang Pingping, and other researchers at the Rural Survey Organization of China’s State Statistical Bureau for data support. Wei Li gratefully acknowledges the financial support from the Darden School Foundation and the hospitality provided by Cheung Kong Graduate School of Business, where he was a visiting professor.

Wei Li
University of Virginia, Cheung Kong Graduate School of Business, and Centre for Economic Policy Research

Dennis Tao Yang
Virginia Polytechnic Institute and State University

The Great Leap Forward disaster, characterized by a collapse in grain production and a widespread famine in China between 1959 and 1961, is found attributable to a systemic failure in central planning. Wishfully expecting a great leap in agricultural productivity from collectivization, the Chinese government accelerated its aggressive industrialization timetable. Grain output fell sharply as the government diverted agricultural resources to industry and imposed an excessive grain procurement burden on peasants, leaving them with insufficient calories to sustain labor productivity. Our analysis shows that 61 percent of the decline in output is attributable to the policies of resource diversion and excessive procurement.

Ten thousand years are too long, seize the day, seize the hour! [Mao Zedong, “Manjianghong—a Reply to Comrade Guo Moruo,” 1963]

I. Introduction

In China, the world’s most populous country that was barely self-sufficient in food supply, the unthinkable happened: National grain output plunged by 15 percent in 1959 and by another 16 percent in the following two years. The government, which ran a closed economy, neither requested nor accepted international assistance. Famine soon raged across China.

The turn of events in China in the late 1950s was dramatic. With much fanfare, the new Communist government launched the Great Leap Forward (GLF) movement in 1958. In its New Year’s editorial, the People’s Daily—the official newspaper of the Chinese Communist Party— proclaimed that the GLF would propel China to surpass Great Britain in industrial production in 15 years and the United States in 20 or 30 years. The nation was soon propelled to a state of exuberance, as news about extraordinary gains in agricultural and industrial production broke out across the country. It appeared that even the seemingly lofty GLF goal could be achieved much sooner. But as the first signs of famine emerged in the winter of 1959, grim reality gradually set in. Years later, demographers who extrapolated mortality trends in China estimated the total number of premature deaths during the GLF famine at between 16.5 and 30 million.[1] Even by the most conservative estimate, this famine ranked the worst in the loss of human lives in recorded world history.[2]

Since the release of official data in the late 1970s, this catastrophe has attracted much attention from social scientists.[3] Recent empirical research has concentrated on the causes of the famine, taking food shortage as a given.[4] This paper departs from the literature by focusing on the fundamental issue: What caused the collapse in grain output?

The postmortem official explanation puts the blame mainly on bad weather (Chinese Communist Party Central Committee 1981) and refers to the period 1959–61 as “three years of natural calamities.” Using meteorological data collected independently, Kueh (1995) finds that bad weather was a contributing factor. But he notes that bad weather of similar magnitude in the past did not produce such a serious reduction in aggregate grain output. Kueh’s finding suggests that there were other important factors. Piece by piece, researchers have identified a number of plausible policy factors. They include reductions in labor and acreage used in grain production (e.g., Peng 1987; Yao 1999), implementation of radical programs such as communal dining (e.g., Yang 1996; Chang and Wen 1997), and reduced work incentives due to the formation of the people’s communes (Perkins and Yusuf 1984). Another policy factor, identified by Lin (1990), is the deprivation of peasants’ rights to exit from the commune. Lin argues that the threat of withdrawal from an agricultural collective by harder-working members helps discipline would-be shirkers. The removal of exit rights destroyed this self-enforcing discipline, reduced work incentives, and hence contributed to the fall in grain output.[5] To date, however, few studies have assessed in a systematic manner the relative quantitative effects of these and other possible factors on grain output, leaving a significant gap in our understanding of the GLF crisis. The paucity of systematic empirical research is perhaps due in part to the lack of a consistent framework for analyzing GLF policies.

In this paper, we formulate a dynamic model of central planning that rationalizes the observed GLF policies and identifies additional factors that may have contributed to the collapse of output. Given the government’s objective of rapid industrialization, the observed policies are consistent with a false premise ingrained in the dominant Soviet economic ideology that collectivization would transform Chinese agriculture from small household farming into large-scale mechanized production, achieving a great leap in productivity.[6] The leap in productivity is what the increasingly impatient central planner wanted. With it, the central planner could extract more surplus (or taxes) from the peasantry to fund an accelerated industrialization campaign. Our model predicts that the impatient central planner, believing in the magic power of collectivization, would divert labor (and other resources) from agriculture to industry and impose excessive burdens of grain procurement on the rural population. Diversion of resources reduces agricultural output directly. Excessive procurement, when combined with an actual reduction in productivity caused by collectivization, significantly reduces food available for consumption in rural areas, leading to a severe nutritional deficiency among rural workers. The resulting reduction in physiological capacity to carry out manual labor would in turn reduce the quality of labor input in growing next year’s crops, leading to an additional decline in production. As we shall show later, the model’s prediction of the dynamic progression of the GLF crisis is consistent with the stylized facts in the data.

To test our hypothesis that the GLF policy package—diversion of agricultural resources and excessive procurement—was responsible for a significant portion of the collapse in grain output, we compiled a province-level panel data set from published sources. We also conducted a retrospective survey in 1999 to acquire additional data from local data archives and agricultural experts. Using these data, we estimate a production function that takes into account both the quantity and quality of factor inputs for assessing the role of various factors in determining changes in grain output between 1952 and 1977. By including as explanatory variables in the production function not only conventional inputs and nutritional status of agricultural workers but also climate conditions and other institutional variables, we are able to test both existing and new hypotheses under a unified framework and assess the relative contributions of various factors to the collapse and the subsequent recovery of grain output.

Our findings suggest that the most important causal factor is the diversion of resources from agriculture, which was responsible for 33 percent of the collapse of output between 1958 and 1961. Excessive procurement of grain, which decimated the physical strength of the peasantry, is the next-largest contributor, accounting for 28.3 percent of the decline in output. Bad weather did play a role, contributing to 12.9 percent of the collapse in production. The crisis thus had the marks of a perfect storm.

Agricultural crises and associated famines have long occupied the attention of scholars. While natural disaster has been a leading cause of many crop failures, Rosen (1999) and this study show that bad judgments can also be fatal. For the Irish famine that Rosen studied, erroneous expectation on the productivity of seed potatoes provoked oversaving, which delayed possible substitution of other crops and led to a sharp reduction in the following year’s food supply. Unlike Ireland, China had a diversified crop portfolio and a huge land mass. It therefore 844 journal of political economy had natural hedges against natural calamities. But through collectivization and the imposition of central planning, the Chinese government introduced a systemic risk: As decisions became centralized, any policy failure would have nationwide repercussions. During the GLF, falsified statistics combined with the central planner’s fanciful vision (which encouraged statistical gamesmanship in the first place) led to massive diversion of resources from agriculture and excessive grain procurement with nationwide disastrous consequences. What makes the Chinese experience unique is that the GLF catastrophe was largely the result of a systemic failure in central planning.

II. Development Strategy and Rural Institutions

Devastated by a century of turmoil and wars, the China that the Communists took over in 1949 was a desperately poor agrarian economy with hardly any industrial assets. Nearly 90 percent of the population lived in rural areas, toiling on small plots of land using century-old labor-intensive farming technology. As the economy started to recover, the new government swiftly adopted a Soviet-style, heavy-industry oriented development strategy in 1952. To fund rapid industrialization, most investable surplus had to be extracted from the vast peasant population. Agricultural productivity had to be raised quickly in order to free up resources for industrial development. In a speech on July 31, 1955, Chairman Mao drew the link between industrialization, grain production, and collectivization:

[Some] comrades fail to understand that socialist industrialization cannot be carried out in isolation from the cooperative transformation of agriculture. In the first place, as everyone knows, China’s current level of production of commodity grain and raw materials for industry is low, whereas the state’s need for them is growing year by year, and this presents a sharp contradiction. If we cannot basically solve the problem of agricultural cooperation within roughly three five-year plans, that is to say, if our agriculture cannot make a leap from small-scale farming with animal-drawn implements to large-scale mechanized farming, ... then we shall fail to resolve the contradiction between the ever-increasing need for commodity grain and industrial raw materials and the present generally low output of staple crops, and we shall run into formidable difficulties in our socialist industrialization and be unable to complete it. (Mao 1977, 5:196–97)

For the central planner, industrialization could not proceed without a great leap forward in agriculture, which in turn could not happen if the traditional household farms were not transformed into large-scale collectives ready to implement mechanized farming.

Starting in 1953, at the urging of the central government, local cadres, eager to demonstrate their revolutionary zeal, rushed to create cooperatives.[7] While, in principle, peasants wishing to exit agricultural producers’ cooperatives were allowed to do so, only 3.7 percent of rural households remained independent by the end of 1956.[8] With the launch of the GLF on January 1, 1958, the government amalgamated smaller cooperatives into 26,500 “people’s communes,” with each encompassing thousands of households.

Believing that collectivization significantly boosted agricultural productivity, the central government exhorted local cadres to “overcome reactionary conservatism” (People’s Daily, September 10, 1958). Local cadres responded by outdoing each other in making wild, baseless claims about grain yield. On the basis of these falsified claims, grain output in 1958 was forecasted to grow to 525 million metric tons from just 195 in 1957! “Actual” output was initially pegged at a more modest 375 million metric tons but was revised downward twice—first to 250 on August 22, 1959, and then to 200 in 1979.[9]

Under the illusion that the collectivization drive had solved China’s food problem permanently, the government diverted a large amount of rural labor from agriculture to industry.[10] In 1958, 16.4 million peasants, about twice the size of the industrial labor force in 1957, were relocated to cities to support the expansion of industry and construction. In the winter of 1957–58, the government also mobilized over 100 million peasants to undertake large irrigation and land reclamation projects and to build and operate “backyard iron furnaces.”[11] As shown in table 1, the agricultural labor force was reduced by 38 million between 1957 and 1958. These diverted laborers were likely the more productive, leaving less productive peasants to toil with agricultural chores. The diversion resulted in a neglect of agricultural work in many regions, sometimes leaving grain to rot in the field.[12]

Table 1. Aggregate Grain Output and Agricultural Inputs in China, 1952–77

Year	Grain Output (Million Tons) (1)	Grain Procurement (Million Tons) (2)	Retained Grain per Capita (kg/Person) (3)	Rural Labor (Millions) (4)	Area Sown with Grain (Million Hectares) (5)	Draft Animals (Million Head) (6)	Farm Machinery (Million HP) (7)	Chemical Fertilizer (Million Tons) (8)
1952	164	33	260	173	124	76	.3	.08
1953	167	47	242	177	127	81	.4	.12
1954	170	51	228	182	129	85	.5	.16
1955	184	48	256	186	130	88	.8	.24
1956	193	40	284	185	136	88	1.1	.33
1957	195	46	273	193	134	84	1.7	.37
1958	200	52	268	155	128	78	2.4	.55
1959	170	64	193	163	116	79	3.4	.54
1960	143	47	182	170	122	73	5.0	.66
1961	148	37	209	197	121	69	7.1	.45
1962	160	32	229	213	122	70	10	.63
1963	170	37	231	220	121	75	12	1.0
1964	188	40	256	228	122	79	13	1.3
1965	195	39	261	234	120	84	15	1.9
1966	214	41	282	243	121	87	17	2.3
1967	218	41	281	252	119	90	20	2.4
1968	209	40	261	261	116	92	22	2.7
1969	211	38	259	271	118	92	26	3.1
1970	240	46	282	278	119	94	29	3.4
1971	250	44	293	284	121	95	38	3.8
1972	241	39	298	283	121	96	50	4.3
1973	265	48	293	289	121	97	65	4.8
1974	275	47	303	292	121	98	81	5.4
1975	285	53	304	295	121	97	102	6.0
1976	286	49	306	294	121	95	117	6.8
1977	283	48	300	293	120	94	140	7.6

Source.—Cols. 1, 2, and 4–6 are taken from Ministry of Agriculture (1989); cols. 7 and 8 are taken from Wen (1993); and col. 3 is the result of dividing the difference between cols. 1 and 2 by the rural population.

With attention abruptly shifted from the problem of food shortage to the seemingly insurmountable problem of storing excess grain, the government encouraged communes to allocate more arable land to cash crops. Table 1 shows that the area sown with grain was reduced by more than 13 percent between 1957 and 1959. At the same time, fearing communalization without fair compensation, peasants reduced their stock of draft animals—the most important piece of capital in Chinese agriculture in the 1950s—by 10 million head between 1956 and 1958. Despite the rapid adoption of farm machines and chemical fertilizers in agriculture during this period (table 1), the use of modern inputs remained low. The government also encouraged communes to establish communal kitchens that provided members with free meals, resulting in a great deal of food waste (Yang 1996).

Ecstatic about the sharp increase in grain yields, the government increased state procurement of grain.[13] Table 1 shows that grain procurement increased from 46 million metric tons in 1957 to 64 million in 1959, even as grain output had actually fallen in 1959![14] Net export of grain was raised from an average of 2.11 million tons between 1953 and 1957 to 3.95 million tons in 1959. Grain retained in rural areas fell sharply from 273 kilograms (kg) per capita in 1957 to 193 kg in 1959, and further down to 182 kg in 1960. Since grain was the primary source of food energy in China at the time, the drop in per capita food availability coincided with the onset of the GLF famine. Estimates of calorie intake by Ashton et al. (1984) show that daily per capita availability of food energy in China fell from over 2,100 calories in 1957 to about 1,500 calories in 1960, or equivalent to less than 1 pound of cereals per day.[15] Reduction in calorie intake has been found to reduce a particular dimension of human capital—physical capacity to carry out manual work—and therefore adversely affects labor productivity (see Strauss 1986; Dasgupta 1993; Strauss and Thomas 1995). Becker (1996) reports that in villages a few miles from Beijing, peasants who survived the initial food shortage in 1959–60 were too weak to plant or harvest new crops. Indeed, grain output fell further in 1960 and remained low in 1961, even as the government dramatically reduced grain procurement (table 1).

In early 1959, as the government gradually learned of the severity of the agricultural problems, it started to moderate its radical policies.[16]In 1960, it reduced the procurement of grain in the countryside by 10 million tons (table 1). It sent tens of millions of people back to the countryside, raising the rural labor force by more than 50 million between 1958 and 1962. It also reduced the size of rural collectives, making each production brigade (usually fewer than 100 households) responsible for its own finances. Beginning in 1965, the government instituted a procurement stabilization program, setting grain procurement at just over 40 million metric tons per year. It also reversed its grain export policy and imported, on average, 4.2 million metric tons of grain per year between 1961 and 1966 and 2.1 million metric tons per year between 1967 and 1976. Grain output began to recover in 1961 but did not surpass its pre-GLF level of 195 million metric tons (recorded in 1957) until 1966, the first year of yet another political upheaval—the Cultural Revolution.

III. The Model

To better understand the nature of the GLF crisis, we set up a dynamic model of central planning that consists of an agricultural sector and an industrial sector. For simplicity, we assume that (a) the agricultural sector uses labor as the only factor input to produce a single output, grain;[17]and (b) the economy’s labor supply is normalized to be one. The government allocates labor L_t to grain production and the remainder 1 L_t to industrial production in each year t. Given L_t ^! 1 at time t, the effective agricultural labor is L*_t ^p L h_{t t}, where h_t ¹ 0 is a measure of each worker’s physical capacity in year t—a specific form of human capital that is relevant here.[18] Since a low level of calorie intake can lead to incapacity to perform farming tasks, a laborer’s work capacity in any year t should depend on his food consumption, c_t, in that year. Hence, following the previous literature (e.g., Bliss and Stern 1978a, 1978b; Strauss 1986), we specify the physical capacity of a worker as an increasing function in c_t, that is, h_t p f(c_t) and f (c_t) ¹ 0.

We also assume that grain production exhibits constant returns to scale in effective labor. The aggregate grain output is thus Q _t p aL f_t (c_t), where a is a productivity parameter, which depends in general on both the technology and the organization of production. Grain output per worker is then q_t p af(c_t). When the government procures (i.e., taxes) p_t from each agricultural worker after the harvest in period t, the retained grain g_t { af(c_t) p_t is saved for consumption in the subsequent period:[19]

ct1 p gt { af(ct) pt. (1)

The industrial sector uses labor as a primary input and grain as an intermediate input. Assume that the technology in industrial production is Leontief: One unit of industrial output requires the use of one unit of labor and m units of grain in production. Therefore, with 1 L_t units of labor in the industrial sector, the industrial output in year t is 1 L_t if m(1 L_t) or more units of grain are used in production.

The government maximizes a discounted flow of industrial output, t_p0 b^t(1 L_t), subject to the constraint that there must be enough grain to feed the industrial workforce and to use as an intermediate input for industrial production in each year. The parameter b ^! 1 is the government’s discount factor. When the government extracts p_t amount of grain from each agricultural worker, the food constraint can be written as

p L_{t t} ≥ (m n)(1 L_t), (2)

where n is the food entitlement for each urban industrial worker.[20]

Given its objective function, the government should allocate just enough labor to agricultural production so that the constraint (2) is binding each year. Thus an optimal amount of labor allocated to agriculture in any year t should be L_t p (m n)/(p_t m n). By combining this constraint and (1), we can rewrite the central planner’s objective as

t af(ct) ct1

U pb . (3) tp₀ af(c_t) c_t1 m n

The central planner’s optimal policy is the solution to the following Euler equation for any given initial condition c ₀:[21]

abf (ct1) paf(ct1) ct2 m n] . (4)

By substituting in c_t2 ^p c_t1 ^p c_t ^p c¯, we find that any stationary point of the system must satisfy f (c¯) p (ab)¹. It can be shown that the dynamic system has an asymptotically stable steady state c¯ if f (c_t) ^! 0 in the neighborhood of c¯. This stability condition requires that food consumption as an investment in work capacity exhibits diminishing returns around the steady state. Since stability implies that f is a decreasing function, the steady-state work capacity h¯, and hence grain output per worker q¯, should therefore increase with grain productivity a and with the central planner’s discount factor b that measures his patience.

The properties of the steady state are consistent with Mao’s statement on the link between agricultural productivity and industrial development. An increase in agricultural productivity raises grain output available for procurement and rural consumption and therefore should in general increase procurement and investment in work capacity. The result would be a permanent increase in grain available for urban consumption, allowing the government to reallocate some labor to industry permanently. A more patient central planner would procure less aggressively in order to raise rural labor’s work capacity, and hence grain output per rural worker, to a permanently higher level than a less patient one.

In the remainder of this section, we show that the radical GLF policies can be formulated by an increasingly impatient central planner relying on the false promise on the impact of collectivization on productivity. We solve the dynamic model numerically and simulate the government’s “optimal” decision making during the GLF and the economy’s dynamic responses. We select the parameter values that characterize the economy on the basis of empirical findings presented later in the paper; see Appendix B for more details.

Start with the postwar recovering economy at year t p 1, with a low food consumption c₁ p 8 and the steady state c¯ p 10. The government first pursues its optimal policy knowing what the true agricultural productivity is. Figures 1b and d show that grain output rises from year 1 to year 4 as the peasants’ per capita consumption of food recovers from its wartime low. Suppose in year 5 that the government becomes more impatient—its discount factor b falls from 0.9 to 0.8—and launches the GLF movement, believing that collectivization would permanently increase agricultural productivity a by 50 percent. But in reality we assume that a permanently falls by 2 percent.

Because a less patient government places a higher value on an immediate increase in industrial output than on future increases, it is willing to extract more resources from agriculture today to speed up industrialization. Combining its impatience with its expectation of a great leap in agricultural productivity, it “optimally” diverts agricultural labor to industry in year 5 (fig. 1a) and raises grain procurement (fig. 1b). But with a realized lower a and less agricultural labor, both output per agricultural worker and aggregate output fall in year 5 (figs. 1b and d). The procurement turns out to be excessive in year 5 (fig. 1b), causing food consumption in year 6 to fall sharply (fig. 1b). The resulting precipitous fall in work capacity (fig. 1c) in turn causes a sharp reduction in grain output per agricultural worker in year 6 (fig. 1b).

In year 6, under the assumption that the government learns the true value of a and restores its patience to b p 0.9,[22] it “optimally” reallocates labor back to agriculture (fig. 1a) and reduces the procurement (fig. 1b). But as h_t reaches the lowest point in year 6, the aggregate grain output falls to its lowest level (fig. 1d), despite the increase in agricultural labor. As food consumption begins to recover from year 7 on (fig. 1b), work capacity, output, procurement, and consumption all begin to recover and gradually converge to a lower-level steady-state equilibrium associated with the lower productivity under the collective institution.

The described dynamics are consistent with the aggregate data presented in Section II. Our analysis thus suggests that diversion of resources and excessive procurement as rationalizable GLF policies are sufficient to generate the dynamic patterns observed in the data. To assess quantitatively the contribution of diversion of resources and excessive procurement to the collapse of grain output and to evaluate their relative importance compared to other potential contributing factors, we turn next to the empirical analysis.

IV. Data and Hypotheses

We compiled from various published sources a panel data set on grain production and procurement at the provincial level. To acquire unpublished data needed for this study, we also conducted a retrospective survey in each province. The survey collected information on weather conditions, average size of production units, and official agricultural policies from sources including provincial data archives and interviews with agricultural experts. Appendix A provides more information on data sources and the survey.

Our analysis focuses on the period between 1952 and 1977 because 1952 was the first year in which systematic data collection began in many provinces and 1977 was the last year prior to the decollectivization reforms. Table 2 reports sample averages of grain output and agricultural inputs from 25 provinces for each year between 1952 and 1977. Farm capital is a variable constructed to measure in equivalent power units (millions of horsepower) the sum of all farm machines and draft animals used in agricultural production. With the exception of sown area, data on inputs are available only in the amounts used in all agricultural activities, including the production of cash crops. The reported agricultural inputs in table 2 should in general be higher than those actually used in grain production. This is likely a minor measurement problem, however, since most agricultural inputs, for example, about 85 percent of sown areas (table 2), were actually used in the production of grain during our sample period. In the empirical analysis, we shall specify a procedure to control for possible measurement errors.

The provincial statistics in table 2 are consistent with the aggregate statistics in table 1. During the GLF period, there was a sharp reduction in grain output and in the use of traditional inputs—labor, land, and draft animals. While the provincial data also reveal rapid increases in fertilizer use throughout the sample period, the rapid increase in the use of farm machines could not fully compensate for the decline in draft animals during the GLF, since the aggregate farm capital fell steadily during the GLF period.

Table 3 presents summary statistics of weather and policy variables. Below we give a brief description of these variables and the testable hypotheses associated with them.

Resource diversion.—Input diversion has both quantitative and qualitative dimensions. The declines in sown area, labor, and farm capital during the GLF, as documented in table 2, measure the extent of quantitative diversion. What is not apparent in the data is that relatively more productive agricultural workers were often assigned to large irrigation and land reclamation projects and to backyard steel mills. Even those who were assigned to farming might also devote a fraction of their time to supporting GLF projects. Since we have data only on steel and iron production in each province, we use the incremental steel and iron output between 1956 and each year from 1957 to 1964 as a proxy for the unobserved diversion of rural labor to nonagricultural GLF projects. Column 1 of table 3 indicates that there was a temporary surge in steel and iron output during the GLF between 1958 and 1961.

Procurement and nutrition effects.—While we do not observe peasant food consumption directly, we do have data on procurement for each province in each year. Since grain consumed during the current planting season must come from retained grain (total grain output minus total procurement) from previous harvesting seasons, we use lagged values of retained grain as a measure of availability of food for the current year. Between 1959 and 1961, as column 2 of table 3 reveals, the retained grain per capita plunged to its lowest levels as a result of production declines and excessive procurement.

Table 2. Provincial Averages of Grain Output and Agricultural Inputs, 1952–77

Year	Grain Output (Million Tons) (1)	Rural Labor (Millions) (2)	Area Sown with Grain (Million Hectares) (3)	Farm Capital (Million HP) (4)	Draft Animals (Million Head) (5)	Machine Power (Million HP) (6)	Chemical Fertilizer (Million Tons) (7)	% Acreage Irrigated (8)	% Acreage Sown with Grain (9)
1952	6.46	8.14	76.1	1.46	2.04	.01	.01	19.5	88.4
1953	6.60	8.29	77.8	1.57	2.17	.01	.02	20.1	88.7
1954	6.49	8.17	76.8	1.62	2.27	.03	.03	22.5	87.8
1955	7.05	8.31	77.3	1.72	2.38	.05	.04	23.2	86.7
1956	7.24	8.47	81.1	1.72	2.35	.08	.05	24.3	87.0
1957	6.96	8.53	79.6	1.71	2.30	.11	.07	24.8	86.7
1958	7.42	8.45	76.1	1.69	2.21	.13	.10	31.5	85.5
1959	6.36	8.34	69.2	1.64	2.07	.20	.11	28.4	82.8
1960	5.41	8.26	72.7	1.59	1.90	.25	.14	28.8	83.7
1961	5.16	8.33	72.3	1.56	1.77	.34	.14	29.7	86.9
1962	5.84	8.57	72.3	1.59	1.72	.39	.16	30.8	87.9
1963	6.28	8.79	71.8	1.70	1.77	.46	.22	31.5	87.5
1964	6.99	8.96	72.5	1.83	1.85	.54	.26	32.2	86.9
1965	7.89	9.13	71.1	1.95	1.91	.62	.34	33.2	85.2
1966	8.34	9.34	71.7	2.11	1.98	.72	.43	34.0	84.5
1967	8.45	9.53	70.7	2.30	2.06	.86	.48	35.1	84.3
1968	8.17	9.75	68.9	2.47	2.12	.99	.50	36.0	84.4
1969	8.15	10.02	69.7	2.66	2.17	1.14	.58	36.9	84.5
1970	9.43	10.27	70.6	2.97	2.22	1.41	.67	38.3	84.8
1971	9.94	10.44	71.5	3.36	2.22	1.81	.76	39.2	84.6
1972	9.63	10.56	71.8	3.78	2.21	2.24	.84	40.0	83.6
1973	10.63	10.72	71.5	4.26	2.23	2.71	.94	41.0	82.9
1974	10.95	10.90	71.4	4.79	2.23	3.23	.99	42.2	82.6
1975	11.43	11.03	71.4	5.35	2.22	3.80	1.09	44.1	82.2
1976	11.39	11.12	71.3	5.94	2.20	4.40	1.24	45.4	81.5
1977	11.25	11.20	71.1	6.57	2.18	5.06	1.43	49.1	81.5

Note.—Data are taken from various published sources for 25 Chinese provinces (see App. A). The three largely urban municipalities (Beijing, Shanghai, and Tianjing) and the two autonomous regions (Tibet and Xinjiang) are not in the sample.

Table 3. Provincial Averages of Policy and Weather Variables, 1952–77

Year	Steel and Iron Output (10,000 Tons) (1)	Retained Grain per Capita in Rural Areas (kg/Person) (2)	Weather Conditions{1} (3)	% Provinces That Removed Exit Rights (4)	Size of Production Units (Households) (5)
1952	4.8	289
1953	6.3	282
1954	7.9	251	3.33	20	22
1955	10.2	271	2.58	20	33
1956	16.0	306	3.17	44	162
1957	19.1	257	3.42	60	179
1958	30.4	280	2.71	60	2,675
1959	46.9	210	3.54	64	1,696
1960	62.6	179	4.00	64	1,751
1961	31.0	186	3.95	64	354
1962	23.8	214	3.39	64	41
1963	27.2	230	3.09	64	30
1964	34.4	244	2.70	64	31
1965	43.7	278	2.74	64	33
1966	54.7	284	2.58	68	31
1967	36.8	289	2.58	68	31
1968	32.6	260	2.83	72	35
1969	47.5	249	2.83	72	36
1970	63.3	278	2.70	68	37
1971	76.0	297	3.13	68	49
1972	83.5	276	3.41	68	50
1973	90.0	293	2.83	68	39
1974	72.2	314	2.48	68	40
1975	85.4	314	2.91	68	40
1976	73.1	300	3.00	68	41
1977	84.8	296	2.87	64	42
Number of provinces	25	19	25	25	23

Source.—Data in cols. 1 and 2 are taken from published sources, and data in cols. 3–5 are taken from the retrospective survey that covers the years between 1954 and 1977. Availability of data varies across provinces.

Note.—The last row shows the maximum number of provinces for which data are available for each of the variables for the entire sample period.

Weather.—We obtained from our survey an index of annual weather conditions for each province on a scale from 1 to 5, with 1 being very good, 2 good, 3 average, 4 bad, and 5 very bad.[23] Consistent with Kueh (1995), column 3 of table 3 shows that bad weather coincided with the collapse of grain output in the period 1959–61.

Exit rights.—In our survey, we interviewed knowledgeable experts in each province, collecting information on when compulsory participation in rural collectives became an official policy. Column 4 of table 3 reports the proportion of sample provinces that explicitly removed exit rights in each year. Consistent with Kung and Putterman’s (1997) observation, the percentage of provinces with no exit rights increased from 20 percent in 1955 to 60 percent in 1957, indicating that farmers’ rights to withdraw from collective farms became tenuous after the consolidation of the collectivization movement in 1956. However, data on the de jure exit rights that we collected in the survey may not accurately represent the de facto exit rights that peasants had. Because of the hyperpolitical atmosphere surrounding the GLF movement, it is hard to imagine that peasants would dare to exercise their exit rights even if they were not explicitly prohibited. Indeed, compulsory participation, which was believed to have been implemented nationwide after 1958 (Lin 1990), was actually not an explicit official policy in about one-third of the sample provinces.

Size of production units.—To assess the incentive effect of collectivization on agricultural labor productivity, we also collected information on the size of basic production units with independent accounting. Column 5 of table 3 shows that the average number of households per production unit grew from 22 in 1954 to 2,675 in 1958 and then fell to 41 in 1962.

Communal dining and radicalism.—Regional innovations in radicalism, as epitomized by the establishment of communal kitchens, may have wasted a substantial amount of food and hence compounded the nutritional effects of excess procurement on peasants’ work capacity. In the fall of 1958, more than 2.65 million communal kitchens were established (see Chang and Wen 1997). By the end of 1959, the participation rate of peasants in communal kitchens reached an average of 64.7 percent, with a range from 16.7 percent to 97.8 percent across provinces. While communal kitchens operated between 1958 and 1960, data on participation rates are available only for 1959. We therefore use the 1959 participation rates to capture regional variations for the whole GLF period. In addition to food waste, Yang (1996) argues that the cross-province variation in communal dining reflected in large part the variation in the degree of radicalism between provincial leaders, which is systematically related to the degree of involvement in the construction of mass irrigation projects and nonagricultural activities. These physically demanding radical initiatives increased the demand for calories among participating laborers, leading to faster exhaustion of food supplies before the next harvest and thus malnutrition among rural workers (Johnson 1998).

V. Empirical Specification

The joint significance of the factors discussed in determining grain output in China can be estimated with a properly specified production function. For province i in year t, given effective inputs of labor (L_it), land (A_it), farm capital (K_it), and chemical fertilizers (M_it ), the grain output Q _it can be written in a Cobb-Douglas specification as

p p5

lnQ it aX lnXit* qjWitj ui v(t) eit, (5)

XpL,A,K,M j 2

where u_i measures province-specific fixed effects that capture geographical and political factors that affect grain production, v(t) is a parametric function of time measuring time-varying factors that affect the production of all provinces, and e_it is an idiosyncratic error term. The weather dummies, W_it², W_it³, W_it⁴, and W_it⁵, indicate whether the weather conditions in year t are “good,” “average,” “bad,” and “very bad,” respectively. With the weather dummy indicating “very good” weather conditions excluded, the coefficients q_j measure the extent of output loss under less than ideal weather conditions. We expect q₅ ! q₄ ! q₃ ! q₂ ! 0.

Effective inputs are inputs that are allocated to gain production and adjusted for quality or efficiency differences. Efficiency adjustments are important here because we are interested in testing, among other hypotheses, whether nutritional deficiencies have a significant impact on peasants’ work capacity and whether collective institutions reduced peasants’ work incentive. Since effective inputs are not directly observed, we embed in (5) empirical models for measuring effective inputs using available data.

To begin with, we propose the following flexible specification for measuring inputs allocated to grain production, X_it^G, by adjusting the total amount of agricultural inputs available in each year, X_it, using data on the proportion of sown area allocated to grain (G_it):

lnX_it^{G p} lnX_it g_X lnG_it c_Xi, X ^p L, A, K, M, (6)

where g_X is an adjustment parameter, and c_Xi captures input- and province-specific factors that affect the allocation of available inputs between grain and nongrain production. If all inputs are allocated in the same proportion as sown acreage for grain production, we should have g_X p 1 and c_Xi p 0. In general, one expects that the proportion of labor (and other inputs) allocated to grain production would be related to G_it.

During the GLF, not all labor allocated to grain production was actually used in grain production or used to its productive potential. Many factors contributed to the reduction in effective labor input. Their combined effects on effective labor can be flexibly specified as lnL*it p lnLGit lnhit gZ lnZit gEEit gS lnSit gR lnR it. (7)

Consider first the adjustment term, lnh_it, which measures the contribution of nutrition to effective labor input. Here h_t is a function of an average peasant’s current consumption of grain, c_t. In estimation, we use a log-linear specification, lnh_t p dlnc_t, where d is a parameter to be estimated. Because grain consumption in the rural area in the current year is not observed, we measure it using retained grain per capita in rural areas from the previous year, g_i,t1, which equals the difference between per capita output and procurement. Accordingly, the contribution of nutrition to effective labor in year t can thus be reexpressed as

lnhit p dlngi,t1. (8)

By construction, g_i,t1 is likely to be positively correlated with the lagged dependent variable lnQ _i,t1. This correlation may cause a downward bias in d in a fixed-effects panel estimation (Arellano and Bond 1991), an econometric problem that we address later.

Turn next to the rest of the adjustment terms in (7). The average size of production units (Z_it) and the removal of exit rights (E_it) may negatively influence the supply of work effort by encouraging free-riding. Here E_it is a dummy variable, with E_it p 1 indicating the de jure absence of exit rights. We expect g_Z ≤ 0 and g_E ≤ 0. The surge in steel output (S_it) during the GLF years due to the proliferation of backyard furnaces and other nonagricultural projects in the countryside can be used as a proxy for unobserved labor diversion. Additionally, radical programs (R _it), as represented by the degree of adopting communal dining, may have caused food waste and possibly other negative effects on production. Therefore, we expect that g_S ≤ 0 and g_R ≤ 0.

Efficiency adjustment can also be made to land input. Since land is usually more productive with irrigation than without, we use the following flexible quality adjustment,

lnA*it p lnAGit gI lnIit, (9)

where I_it is the proportion of sown area under irrigation. Because efficiency variations in chemical fertilizers and farm capital are unobserved and are presumably small, we make no efficiency adjustment to

MitG and KitG.

By substituting (6)–(9) into (5) and letting u*_i p_X a_{X Xic} u_i and g_G ^p_X g a_{X X}, we derive the following fixed-effects regression model using only observed variables:

lnQ it paA(lnAit gI lnIit)aM lnMit aK lnKit gG lnGit

aL(lnLit dlngi,t1 gZ lnZit gEEit gS lnSit gR lnRit)

p5

q_jW_it^j u*_i v(t)e_it. (10)

j 2

To find an appropriate empirical strategy for estimating equation (10), we need to take into account the main features of Chinese agriculture. Section II indicates that, for the period between 1952 and 1977, resource allocation was centralized, with economic policies formulated at the national level.[24] This contrasts sharply with a market economy in which individual firms make independent production decisions, each taking price signals and local farming conditions as given. With decentralized decision making, changes in economic activities in each individual farm are usually determined more by changes in microeconomic factors, such as output and input prices as well as climate and soil conditions, than by changes in aggregate policy factors. In China, however, since agricultural collectives were under central control, production activities in all provinces were likely determined by the common policy directives formulated at the center. Consequently, we expect that the input and policy variables in (10) exhibit strong time-series comovements across provinces because of the common time-varying factor— the central planning directives.

This conjecture is consistent with the data. In table 4, we report Fstatistics from analysis of variance (ANOVA) of the following fixed-effects specification:

Y

ln it ) p AYt BiY CwY,it Eit (11)

Yi,t1

for all continuous input and policy variables in (10), where Y p L, A, I, G, K, M, g, Z, and S. Here A^Y_t and B_i^Y represent time- and provincespecific effects, C_w^Y_,it measures the effect of weather conditions in years t 1 and t,[25] and E_it is the error term. If decisions were centralized, we would expect time effects to be statistically more significant than province effects, revealing strong comovements in the input and policy variables across provinces. Evidence reported in table 4 confirms this conjecture, showing that time effects clearly dominate province effects in explaining variation in input and policy variables, after we control for weather conditions.[26] The findings also indicate statistically weaker, but nonetheless measurable, regional variations in some input variables, such as labor and farm capital. However, consistent with the central planning conjecture, policy variables (g, S, and Z) show little regional variation.

Table 4. F-Statistics from ANOVA Tests

Dependent Variable (Annual Changes in the Logarithm of)		Categorical Explanatory Variables
	Year	Province	Weather
Sown area	9.57*** (22, 471)	1.28 (23, 471)	1.43* (24, 471)
% acreage irrigated	1.58** (22, 470)	1.16 (23, 470)	1.86*** (24, 470)
% acreage sown with grain	2.09*** (22, 471)	.68 (23, 471)	.72 (24, 471)
Fertilizer	5.74*** (22, 471)	1.11 (23, 471)	.87 (24, 471)
Farm capital	10.45*** (22, 471)	1.52* (23, 471)	1.90*** (24, 471)
Labor	7.34*** (22, 471)	1.70** (23, 471)	.93 (24, 471)
Food availability	9.31*** (22, 369)	.26 (18, 369)	1.34 (24, 369)
Steel production	31.83*** (22, 424)	.10 (23, 424)	1.01 (24, 424)
Production unit size	9.50*** (22, 455)	.13 (23, 455)	.86 (24, 455)

Note.—The numbers in parentheses are numerator and denominator degrees of freedom for each of the listed Fstatistics. The weather variable measures the weather conditions in both the current year and the previous year.

* Statistically significant at the 10 percent level.

** Statistically significant at the 5 percent level.

*** Statistically significant at the 1 percent level.

The central planning mechanism that generated our data offers implications for choosing an appropriate empirical methodology. To the extent that the input and policy variables in (10) contain a common time-series component, we should be concerned about potential multicollinearity in our specification. In particular, we expect multicollinearity between v(t) and the input and policy variables. If v(t) is modelled using year dummies, the most flexible parametric specification, it may well capture the common time-series components induced by central planning that are also present in the input and policy variables, making it difficult to identify the effects of these variables. In general, econometricians (e.g., Arellano 2003, 61) suggest the exclusion of time dummies in short panels when the effects of macro-level explanatory variables are of substantive interest. Following this advice, we propose a parsimonious specification v(t) p vt to capture the effect of technological changes between 1952 and 1977 (e.g., the adoption of high-yield and disease-resistant varieties of crops), while minimizing the influence of multicollinearity. In estimation, we perform diagnostic tests on multicollinearity.

However, centralized decision making also makes an econometrician’s job easier. Since allocation decisions at the provincial level were made by the central planner, they are unlikely to be correlated with the idiosyncratic error e_it. While resource allocation decisions could be made on the basis of each individual province’s specific features when they are observed, it would be difficult for the central government to get upto-date information on the idiosyncratic shock e_it. The fact that the government continued its GLF policies in 1960 after experiencing a precipitous fall in grain production in many provinces in 1959 suggests that the government did not have access to up-to-date local information, or that it failed to act on it.

To the extent that decision variables are uncorrelated with the idiosyncratic error e_it, equation (10) represents a dynamic fixed-effects panel regression with exogenous input, policy, and weather variables on the right-hand side. The dynamics arises because food availability in year t, g_i,t1, is equal to the difference between grain output and grain procurement in year t 1. Since g_i,t1 is likely positively correlated with the lagged dependent variable, lnQ _i,t1, a standard fixed-effects regression applied to our short panel (1952–77), as argued in Arellano and Bond (1991), will likely underestimate a d_L . To obtain consistent estimates, we adopt a simple instrumental variables approach. The instruments are lagged exogenous variables that are correlated with g_i,t1 but not with the demeaned idiosyncratic error, e_it (_t e_it/T).

Finally, we note that the idiosyncratic error terms, e_it, are unlikely to be independent between provinces. Owing to geographic affinity, an idiosyncratic shock in one province, say the emergence of a locust attack, may well spread into neighboring provinces, creating cross-sectional correlation in the idiosyncratic shocks. It is thus important that we obtain robust standard errors to account for clustering on year in estimation.

VI. Empirical Findings

Table 5 reports fixed-effects estimates of equation (10) and their robust standard errors in five variant specifications. Column 1 presents the ordinary least squares (OLS) estimates of the baseline regression, which includes only the four conventional agricultural inputs as explanatory variables. The results indicate that all conventional inputs contribute positively and significantly to grain output, with labor accounting for the largest input share. The sum of input coefficients is 1.04, which is statistically indistinguishable from one. We thus cannot reject the null hypothesis of constant returns to scale in Chinese agriculture. The estimated coefficient on the proportion of acreage sown with grain (lnG_it) is small and statistically indistinguishable from zero, implying that, on the margin, available labor, capital, and fertilizers were allocated mostly to grain production. This result also holds true in the other four specifications.

The specification in column 1 does not include any variables that measure time effects. To examine the impact of central planning and aggregate weather fluctuations on grain production, we add year dummies to the baseline regression. Figure 2 plots the estimated time effects: figure 2a shows the effects without controlling for a time trend, and figure 2b shows the detrended effects. It is worth noting the similarity between the detrended time effects and the simulated output changes in figure 1d. However, while useful in shedding some light on the effects of aggregate GLF policies and weather fluctuations, the inclusion of year dummies makes it difficult to identify separately the effects of specific GLF policies and weather conditions. The main reason, argued in Section V, is the multicollinearity generated by correlation between the time effects, the common time-series component in input and policy variables, and aggregate weather fluctuations. Table 4 provides strong evidence of correlation between the time effects and input and policy variables. Our calculation pegs the correlation coefficient between the time effects and the effects of weather fluctuations based on estimates in column 4 of table 5 at 0.68 with statistical significance at the 1 percent level. Diagnostic tests suggest nearly perfect multicollinearity between the year dummies and other covariates included in specifications 2–4 of table 5. These results suggest that most of the time effects can be accounted for by the common time-series component in input and policy variables and in weather conditions. Given the paper’s objectives, our discussion below focuses on the contributions of specific policy factors and weather conditions that are estimated on the basis of specifications that include only a time trend.

Column 2 of table 5 adds to the baseline model weather and irrigation variables, as well as policy variables emphasized in the existing literature.

Table 5. Estimation of Grain Production Function in China, 1952–77

Dependent Variable: ln(Grain Output)

Fixed-Effect Instru-

Fixed-Effect OLS mental Variables

Explanatory

Variable	(1)	(2)	(3)	(4)	(5)
ln(sown area)	.206** (.104)	.448*** (.088)	.479*** (.088)	.474*** (.092)	.442*** (.087)
ln(% acreage irrigated)		.131*** (.029)	.129*** (.027)	.127*** (.025)	.110*** (.025)
ln(% acreage sown with grain)	.019 (.059)	.114 (.065)	.059 (.083)	.055 (.097)	.091 (.092)
ln(fertilizer)	.012* (.007)	.033*** (.011)	.022** (.010)	.019* (.010)	.025** (.010)
ln(farm capital)	.245*** (.030)	.224*** (.027)	.160*** (.024)	.138*** (.030)	.158*** (.028)
ln(labor)	.578*** (.107)	.532*** (.125)	.311*** (.087)	.284*** (.088)	.343*** (.100)
ln(food availability)			.180*** (.050)	.267*** (.077)
Tercile 1 (low)					.271*** (.108)
Tercile 2 (middle)					.246* (.137)
Tercile 3 (high)					.332** (.167)
ln(steel production)			.093*** (.027)	.099*** (.028)	.090*** (.028)
ln(communal dining)		.083 (.073)	.045 (.031)	.076** (.037)	.034 (.039)
ln(production unit size)		.008* (.005)	.014** (.007)	.013** (.006)	.012** (.005)
No exit (de jure)		.006 (.022)	.026 (.019)	.024 (.018)	.038 (.023)
Good weather		.016 (.021)	.006 (.022)	.011 (.017)	.014 (.026)
Average weather		.048** (.020)	.036 (.023)	.034* (.020)	.044* (.025)
Bad weather		.116*** (.027)	.080*** (.026)	.076*** (.023)	.081*** (.023)
Very bad weather		.169*** (.031)	.161*** (.033)	.156*** (.036)	.158*** (.035)
Time trend		.107*** (.042)	.018 (.033)	.002 (.037)	.014 (.034)
R2	.704	.764	.805	.800	.791
Observations	624	551	428	406	406

Note.—Numbers in parentheses are robust standard errors adjusted for clustering on year.

* Statistically significant at the 10 percent level.

** Statistically significant at the 5 percent level.

*** Statistically significant at the 1 percent level.

As expected, irrigation raises grain output, whereas less than ideal weather conditions reduce it. Although the effect of good weather is not statistically significantly different from that of very good weather (the dummy variable omitted as the reference), the realization of average, bad, or very bad weather conditions would reduce grain output by 4.8, 11.6, or 16.9 percent, respectively. We also find that grain output is significantly lower in provinces with higher rates of participation in communal dining, a proxy that we use for regional radicalism. This result is consistent with previous findings of deleterious effects of regional radicalism (Yang 1996). The effects of the other two policy variables, however, merit more discussion.

Consider first the no-exit dummy variable. Lin (1990) hypothesized that the removal of the peasants’ rights to withdraw from the communes in 1958 sharply reduced their work incentives. While the estimated coefficient on the no-exit dummy is negative, consistent with the hypothesis, it is not statistically significant. A plausible interpretation of this inconclusive result is measurement error. The no-exit dummy measures the de jure removal of exit rights (see App. A), which may significantly understate the de facto removal of exit rights across provinces. In the politicized environment surrounding the GLF, it was virtually inconceivable that a peasant could choose to leave the commune, even if there was no official policy prohibiting withdrawal. Turn next to the average size of production teams. While there may be economies of scale arising from the use of farm machines and other modern inputs, collective farming faces serious incentive problems as a result of the egalitarian income-sharing rule and the high costs of monitoring each member’s work effort. Lack of managerial experience in running large organizations may also result in poor performance. While the net effect of the size of production unit cannot be ascertained theoretically, the estimate of the coefficient on the variable is positive but statistically insignificant, suggesting that the larger size of organizations per se did not reduce the quality of labor input.

The OLS and instrumental variables estimates of the full dynamic specification in equation (10), with the addition of food availability and the surge in steel production (resource diversion) variables, are reported in columns 3 and 4. While the signs of the estimated coefficients are mostly consistent with expectations, the inclusion of new variables reduces the magnitude of the estimated coefficient on labor to 0.311 and 0.284 from 0.532 in column 2. This is not surprising. With effective labor measured in the full specification, the marginal productivity of basic (i.e., not augmented) labor should be lower than that of the average labor. There is also a slight drop in the estimates of the coefficients on farm capital and fertilizer, whereas the estimates of the coefficients on other factor inputs remain largely unchanged.

Comparing the OLS and instrumental variables estimates in columns 3 and 4, we notice that they are very close for most coefficients. The most significant difference occurs between the OLS and instrumental variables estimates of the coefficient on food availability: The instrumental variables estimate is substantially larger. This is expected. Since food availability, as an increasing function of the lagged grain output, is negatively correlated with the demeaned error term in our short panel, the OLS estimate is downwardly biased. Since the instrumental variables estimates are expected to be consistent, our discussion below will focus on these estimates in column 4.

A comparison of estimates in columns 2 and 4 reveals that qualitative empirical findings based on column 2 remain valid in column 4. Less than ideal weather conditions reduce grain output markedly. Regional radicalism, epitomized by communal dining, has a negative and now significant effect on grain output. The average size of production units still has a positive and small effect on grain output, lending little support to the argument that a larger team necessarily leads to a net reduction in labor productivity. The estimate of the coefficient on the no-exit dummy is still negative and statistically insignificant. This finding is consistent with previous findings (Lin 1990; Wen 1993) that the removal of exit rights, or more generally the collectivization movement, reduced agricultural productivity. But given the purpose of this paper, we have limited our analysis to the period 1952–77 and therefore cannot take advantage of the decollectivization event after 1978 to measure the negative effect of compulsive, collective institutions.

The two most important findings in column 4 relate to the two newly added variables, steel production and food availability. As expected, the coefficient on steel production, a proxy for labor quantity as well as quality diversions, is negative and statistically significant. An increase in the GLF-led surge in steel output by 10 percent, ceteris paribus, reduces the effective agricultural labor and hence grain output by about 0.99 percent. Given the dramatic surge in provincial average steel output for three consecutive years between 1958 and 1960 (see table 3), this variable alone should explain a good part of the decline in grain output in those years. This finding implies that backyard steel smelters and large land reclamation and irrigation projects represented an important dimension of resource diversion during the GLF. Combined with the fact that the government also directed productive inputs out of the rural sector (see table 2), resource diversion should be a major factor explaining the collapse of grain output.

The estimated coefficient on food availability, a proxy for an average worker’s physical capacity, is positive and statistically significant. This implies, not surprisingly, that better nutrition enhances labor productivity. The magnitude of the estimate is substantial. A 10 percent reduction in retained grain from the previous year would lead to a 2.67 percent drop in grain output in the current year. This finding implies that the severe nutritional deficiency among agricultural workers during the GLF (see table 3) was another important factor explaining the collapse of grain output.

As expressed in (10), the coefficient on food availability is the product of the coefficient on labor and d, where d is the food elasticity of work capacity (see [8]). On the basis of the instrumental variables estimates in column 4, we find that the estimate of d is 0.94 (or 0.267/0.284) with a standard error of 0.48, which is obtained using the delta method. This estimated size of the food elasticity of work capacity is large and consistent with Strauss’s (1986) estimates of the calorie elasticity among Sierra Leone farm households at low levels of calorie intake (e.g., 1,500 per day per person). One can thus infer that nutritional deficiency was a major contributor to the collapse of grain production.

Using microeconomic data, previous studies (e.g., Strauss 1986) also find that the relationship between calorie intake and labor productivity is nonlinear: the calorie elasticity is high at low levels of food consumption. To see whether a nonlinear relationship exists in our aggregate data, we rerun the instrumental variables estimation using a piecewise linear specification to allow food elasticities to vary across the lower, middle, or higher terciles of food consumption. The estimates reported in column 5 of table 5 show that food availability at all three levels has significant effects on grain output. The food elasticities at the lower, middle, and higher terciles of food availability are 0.79, 0.72, and 0.97, respectively, with standard errors of 0.43, 0.49, and 0.61. Given the relatively large standard errors, we cannot reject the null hypotheses that the three estimates are pairwise identical and that they are equal to the estimate of 0.94 based on the simple linear specification. In sum, we find that with aggregate data the food elasticity is high and does not appear to exhibit strong nonlinearity. But there are reasons that this finding is not surprising. One reason may be that we use aggregate rather than household data. Since aggregation masks any consequences of food distribution, there is not necessarily a one-to-one correspondence between household and aggregate food elasticities.[27] Perhaps more important, because of the combination of low agricultural productivity and high procurement burdens, rural food availability was low throughout the central planning period (Lin and Yang 2000). As a result, food elasticities are expected to be high. The fact that peasants in China were barely capable of keeping up with feeding a burgeoning postwar population also helps explain why the GLF crisis had such tragic consequences.

We have so far presented a systematic empirical analysis of the determination of grain output in China between 1952 and 1977. Before we proceed to estimate the extent to which the GLF crisis is attributable to each of the identified factors, it seems prudent to first check the robustness of the results using alternative samples and alternative measures of weather and regional radicalism. In table 6, we present instrumental variables estimates of (10) under these different specifications.

Table 6 Sensitivity Analysis Dependent Variable: ln (Grain Output)

Explanatory Variable	(1)	(2)	(3)	(4)
ln(sown area)	.471*** (.160)	.378*** (.095)	.347** (.157)	.435*** (.093)
ln(% acreage irrigated)	.069** (.027)	.102*** (.025)	.058** (.025)	.116*** (.023)
ln(% acreage sown with grain)	.121 (.210)	.016 (.104)	.010 (.147)	.049 (.099)
ln(fertilizer)	.009 (.016)	.028** (.012)	.013 (.013)	.020** (.010)
ln(farm capital)	.091** (.044)	.117*** (.030)	.162*** (.057)	.141*** (.029)
ln(labor)	.106 (.142)	.347*** (.082)	.235* (.122)	.219*** (.083)
ln(food availability)	.301*** (.088)	.312*** (.082)	.135 (.130)	.270*** (.080)
ln(steel production)	.099*** (.029)	.092*** (.027)	.104*** (.021)	.021 (.019)
ln(communal dining)	.065** (.030)	.079** (.035)	.005 (.055)
ln(time of liberation)				.010*** (.003)
ln(production unit size)	.008 (.008)	.012** (.005)	.017** (.007)	.010 (.006)
No exit (de jure)	.005 (.036)	.019 (.018)	.010 (.037)	.019 (.019)
Good weather	.020 (.027)	.006 (.022)		.014 (.017)
Average weather	.032 (.029)	.037 (.025)		.026 (.019)
Bad weather	.114*** (.032)	.070*** (.028)		.063*** (.023)
Very bad weather	.223*** (.036)	.150*** (.039)		.124*** (.035)
ln(% acreage affected by calamity)			.077*** (.010)
Time trend	.042 (.043)	.001 (.038)	.008 (.053)	.010 (.034)
R2	.531	.801	.543	.811
Observations	207	363	210	406

* Statistically significant at the 10 percent level.

** Statistically significant at the 5 percent level.

*** Statistically significant at the 1 percent level.

To begin with, we would like to know whether our results are sensitive to the selection of the particular time period included in the analysis. Column 1 in table 6 presents the instrumental variables fixed-effects estimates using a shorter time period: 1952–66. We choose 1966 to be an alternative ending year because it marks the beginning of another period of political upheaval in China—the Cultural Revolution. Compared with estimates in column 4 of table 5, the R ² drops to 0.53 from the previous 0.80, as the sample size shrinks from 406 to 207. With the shorter panel, the negative effects of bad and very bad weather appear to be stronger. A plausible explanation is that as the time period is shortened, it is less likely that we would find weather conditions in nonGLF years that are comparable to the extreme weather conditions in GLF years. It is thus likely that some of the policy effects could have been attributed to weather conditions. However, the estimates on the coefficients of the other variables remain mostly unchanged, although their standard errors tend to be larger than those in column 4 of table 5.

Next, we investigate whether our findings are unduly influenced by a few provinces that experienced excessively high mortality during the GLF period. Previous studies (e.g., Lin and Yang 1998) find that provinces with high mortality exhibited some unusual characteristics, such as radical leadership and extreme policies, that our data may not capture. To address this concern, we remove from our sample the three provinces with the highest mortality rates during the GLF period— Sichuan, Anhui, and Guizhou[28]—and reestimate the full model. Reported in column 2 of table 6, the results indicate a fair degree of stability, with all significant coefficients maintaining the same signs as in column 4 of table 5.

We also examine whether our earlier results are sensitive to using an alternative weather variable. The weather dummies used in the regressions in table 5 were collected by us in a supplemental survey (see App. A). One might argue that the information collected may not be comparable across provinces since different respondents might have used somewhat different classification schemes in filling out our survey questionnaire. Responding to this concern, we rerun the instrumental variables regression using the existing official weather index, which measures the sown area affected by natural calamities (see n. 23 for more information on this variable). Given the party line explanation of the GLF disaster, it is likely that crop failures caused by the failed GLF policies may have been attributed to bad weather. As a result, we expect the inclusion of this weather variable to potentially reduce the estimated effects of policy variables. Consistent with this conjecture, the estimates reported in column 3 show that while all estimates have the right signs, the effect of food availability is now much smaller and statistically insignificant. Because about half of the official weather variables are missing in published sources, the sample size shrinks from 406 to 210.

And finally, we remove the rate of participation in communal dining as a proxy for a province’s radicalism during the GLF and replace it with the time of liberation in each province as a proxy. Previous researchers (Yang 1996; Kung and Lin 2003) have found that provinces taken over by the Communist forces at later times were often appointed with more left-leaning leaders. The estimates reported in column 4 are again not systematically different from the estimates in table 5.

Using the estimates in column 4 of table 5, we next assess quantitatively the contributions of various identified factors to changes in grain output during the GLF crisis. To begin, we group various factors into five broad categories: (1) excessive procurement and nutrition as measured by per capita food availability; (2) resource diversion as measured by changes in sown area, labor, capital, and steel production; (3) weather conditions; (4) institutional factors, including communal dining/radicalism, the removal of exit rights, and the average size of production units; and (5) modern inputs, consisting of the use of fertility and irrigation. To assess quantitatively the contribution of each category of factors to the collapse (1958–61) and the subsequent recovery (1961– 66) of grain output,[29] we estimate the effects on grain output of the observed changes in each of the right-hand-side variables in equation (10), using the estimates reported in column 4 of table 5. We report the results in table 7 and provide a brief description of our method in Appendix C.

The results in table 7 suggest that our empirical model fits the data well: The estimated changes account for 66.1 and 70.7 percent of the observed changes in grain output for the two periods. For the collapse between 1958 and 1961, resource diversion was the most important contributing factor, responsible for 33 percent of the observed declines in grain output. The intertemporal effect of excessive procurement and nutrition was the second-largest contributor to the decline, accounting for 28.3 percent of the production shortfall. Adverse weather conditions also played a significant role, reducing food supplies by 12.9 percent. The increased usage of fertilizer and irrigation helped mitigate the negative GLF policies, but their magnitude was small. The effects of institutional or policy factors tended to neutralize each other within the four-year period. Because the participation in communal dining and various radical activities peaked at the end of 1958 and the rectification of the GLF policies led to the closure of most dining halls in 1961 (Chang and Wen 1997), the effect of this variable on grain output was actually positive for the period, which mitigated the negative effects associated with the scale of production. Finally, the de jure removal of exit rights appears to have played a limited role in affecting grain output during the collapse period. But as discussed earlier, the effect of the no-exit policy may have been underestimated.

Table 7. Contribution of Explanatory Variables to the GLF Grain Output Collapse and the Post-GLF Recovery

	The Collapse (1958–61)		The Recovery (1961–66)
Contributing Factors	Changes in ln(Output) (1)	% Contribution to Total Change (2)	Changes in ln(Output) (3)	% Contribution to Total Change (4)
Observed total change	.352	100.0	.445	100.0
Estimated total change	.232*** (.038)	66.1	.315*** (.024)	70.7
Procurement/nutrition	.100*** (.029)	28.3	.042*** (.002)	9.4
Resource diversion	.116*** (.024)	33.0	.165*** (.029)	37.1
Sown area	.023*** (.005)	6.6	.010*** (.002)	2.2
Farm capital	.009*** (.002)	2.5	.041*** (.009)	9.2
Labor	.004*** (.001)	1.2	.035*** (.011)	7.8
Steel production	.080*** (.023)	22.6	.080*** (.023)	17.9
Weather conditions	.045*** (.008)	12.9	.052*** (.012)	14.7
Policy factors	.019 (.026)	5.5	.013** (.006)	3.0
Communal dining/ radicalism	.049** (.024)	13.9	.000	.0
No exit (de jure)	.001 (.001)	.3	.001 (.001)	.2
Production unit size	.029** (.012)	8.1	.012** (.005)	2.8
Modern inputs	.011** (.005)	3.0	.055*** (.017)	12.3
Fertilizer	.009* (.005)	2.6	.028* (.015)	6.4
% acreage irrigated	.0014*** (.003)	.4	.026*** (.005)	5.9
Miscellaneous	.0014 (.0131)	.4	.001 (.016)	.3
% acreage sown with grain	.0008 (.0014)	.2	.002 (.004)	.5
Time trend	.0006 (.0131)	.2	.001 (.015)	.2
Residuals	.119*** (.038)	33.9	.130*** (.024)	29.3

Note.—The numbers in parentheses are robust standard errors.

* Statistically significant at the 10 percent level.

** Statistically significant at the 5 percent level.

*** Statistically significant at the 1 percent level.

It is interesting to observe that the recovery was achieved mainly by allocating massive amounts of resources back to the agricultural sector, something that a central planner knew how to do well. Improved weather conditions and increased use of modern agricultural inputs were also responsible for the rebound in grain output. And finally, the procurement stabilization program implemented after the GLF helped restore peasants’ nutrition and work capacity, which in turn contributed to the recovery.

VII. Conclusion

Throughout history and in different parts of the world, natural disasters have often been blamed as the leading cause of massive crop failures. The Chinese experience was special because the dramatic decline in grain output coincided with the inception of the Great Leap Forward movement as well as a spell of bad weather. Contrary to the official story, which pinned the blame for disaster mainly on bad weather, our theoretical and empirical analysis suggests that the main culprit was the GLF policies.

The dynamic model that we developed in this paper seeks to rationalize the behavior of the government that adopted central planning as the means of organizing economic activities in postwar China. Encouraged by expectations of a great leap in agricultural productivity from collectivization, the government switched to an accelerated timetable for industrialization. With agriculture collectivized in the countryside, the government diverted massive amounts of agricultural resources to industry and sharply raised grain procurement from the peasants. As the great leap in agricultural productivity turned out to be a pipe dream, both resource diversion and grain procurement were excessive. When agricultural inputs were reduced and peasants who carried on farming were left with insufficient food to maintain their productivity, grain output fell sharply. Recovery started gradually only when the GLF policies were reversed.

Combining data from published sources and from our own survey, we are able to construct variables needed for testing the implications of our theory as well as hypotheses proposed in previous studies. By estimating a production function that incorporates both quantitative and qualitative efficiency adjustments made to factor inputs, we find that resource diversion and excessive procurement were the main contributors to the collapse of output. Diversion of resources from agriculture was responsible for 33.0 percent of the decline in grain output for the period between 1958 and 1961. Excessive procurement, which decimated the physical strength of rural workers, was responsible for 28.3 percent of the decline. Bad weather also played a role and was responsible for 12.9 percent of the decline.

The dynamic progression of the crisis observed in the data is consistent with our theoretical predictions. Massive diversion of agricultural resources to industry at the inception of the GLF reduced grain output in 1959. The excessive extraction of food grain from peasants in 1958 and again in 1959 severely reduced food available for consumption in rural areas, igniting a famine in some regions in the winter/spring of 1959. The famine soon spread to much of the countryside in 1960. Weakened by malnutrition, peasants could not exert sufficient labor input into planting or harvesting crops, leading to sharp declines in grain output. Adverse weather conditions exacerbated the collapse of output.

We hope that this study provides not only insights into the tragedy of China’s Great Leap Forward but also a better understanding of the more general relationship between economic system and economic performance. Our research identifies a major weakness in central planning. As decisions became centralized, any policy failure would have economywide repercussions, thereby exposing the economy to new systemic risks. In addition, the centrally planned system as practiced in China in the late 1950s lacked checks and balances and proved ineffective in arresting the momentum of apparently deleterious policy initiatives. The GLF crisis could have been far less devastating had local officials not faced strong political incentives to implement apparently poorly conceived policies and to conceal unfavorable information on local economic performance. However, given the design of the system, the observed policies, no matter how irrational they were to an outside observer, were rationalizable within the confines of the system. By conducting a detailed analysis of China’s GLF disaster, we have therefore come to some understanding about the nature of central planning and the systemic risk to which it exposes the economy.

Appendix A Description of the Survey and Data

A. The Survey

The retrospective survey was conducted by the authors during the summer of 1999 in cooperation with the General Organization of Rural Socio-economic Survey (GORSES), a division of the State Statistical Bureau of China. Members of GORSES’s branch offices in each province implemented the survey. The survey team filled out the questionnaire by first using available historical and statistical records. When archived historical records were incomplete, the team would then conduct an interview meeting to assess, estimate, and supplement the missing data. The interviewees were selected in each province from a pool of local agricultural experts and local academic researchers who were knowledgeable about the history of agricultural production in that province. To ensure that we collected first-hand information, we required that at least two of the interviewees be older than 55. For variables concerning weather, average size of production units, and the evolution of rural institutions, we requested answers to the following questions for each year between 1954 and 1989:

1. What is the name of the basic accounting unit for agricultural production? (a) elementary team; (b) advanced team; (c) commune; (d) production brigade; (e) production team; (f) household.

2. According to official provincial regulations, are farmers permitted to withdraw from their collective production units (e.g. withdraw from elementary collectives)? (a) yes; (b) no.

3. What is the average scale of the basic production accounting units in this province? Please give your estimate on the number of households in a unit.

4. Please rate the overall weather conditions for agricultural production: (a) very good; (b) good; (c) average; (d) bad; (e) very bad.

B. Variable Descriptions

Provincial-level agricultural input and output came mainly from the Compilation of China’s Rural Economic Statistics: 1949–86 (Ministry of Agriculture 1989). When there were missing data, we then searched for information from various volumes of China Statistical Yearbook and Agricultural Statistical Yearbook published by individual provinces in various years. Using multiple sources allowed us to crosscheck the data. Most variables we use are described in the text, with units noted in tables 2 and 3. We give more detailed descriptions to the following variables.

Grain output.—The simple arithmetic sum of the gross physical output of eight main varieties of starches and beans: rice, wheat, corn, potato, sorghum, millet, soybeans, and other coarse grains. Output of each variety is not available from published data.

Sown area.—Land on which crops are planted and from which a harvest is expected. Since land is frequently sown two or more times a year (multiple cropping), sown area is often substantially larger than cultivated area.

Draft animals.—The available numbers are end-of-year head of draft animals. We compute the simple arithmetic mean of the two end-of-year numbers for a more accurate proxy for draft animals for the corresponding calendar year.

Farm capital.—The sum, in equivalent power units, of all farm machines and draft animals in a given year. Measured in millions of horsepower (HP), the formula for aggregation recommended by the State Statistical Bureau is farm capital in million HP p machine power in million kilowatts/0.7457 draft animals in million head # 0.7.

Appendix B Choice of Model Parameters

Model parameters that characterize the pre-GLF economy are chosen as follows. We set bp 9/10, a relatively small discount factor, to reflect the government’s desire for speedy industrialization. We set the work capacity augmentation function as h_t ^p f(c_t) ^p c_t^d, with d^p 0.85, a value that is close to the average of the estimates of d implied by results reported in column 5 of table 5. For the productivity parameter, we set a p 1.8465 and m n p 27.6471 such that, in the steady state, c¯p 10 and the proportion of labor allocated to agriculture is 90 percent.

Appendix C Method for Estimating Factor Contributions

We describe briefly the method that we used to estimate the contribution of each explanatory variable to the collapse in grain output during the GLF and the subsequent recovery. Consider a variable X_j with estimated coefficient gˆ _j. The contribution of this variable to the collapse in grain output in logarithm can be computed as

where DlnX_j,58–61 ^{ lnX_j,61 lnX_j,58 measures the observed changes in the factor over the period 1958–61. For factors not specified in logarithmic form, such as weather, DlnQ_j,58–61 ^pgDˆ _j X_j,58–61. When n explanatory variables (e.g., sown area, capital, labor, and steel production) belong to the same category (e.g., resource diversion), their aggregate effect z on the collapse of production is the sum of each individual effect:

We derive the variance of this aggregate effect on the basis of the variancecovariance of gˆ _j: pn pn

Finally, using (C1) and (C2), we compute the percentage contribution made by X_j, or by a group of factors, to the total observed changes in ln(output) as

where DlnQ _58–61 ^p lnQ ₆₁ lnQ ₅₈. Using the same approach, we also evaluate the contribution of these explanatory variables to the recovery in the period 1961–66.

References

[1] This range of estimates is based on the following research reports, listed in ascending order of the estimated death toll measured in millions: Coale (1981), 16.5; Yao (1999), 18.48; Peng (1987), 23; Ashton et al. (1984), 29.5; and Banister (1987), 30. The variation in the estimates is due to differences in data sources and methods of estimation.

[2] In comparison, the great Irish famine (1845–51) claimed 1.1 million lives, the Bengal famine (1943) 3 million, and the Ethiopian famine (1984–85) between 0.6 and 1 million (see Sen 1981; Ravallion 1997).

[3] Evidence of increased research interests includes a 1993 symposium issue of the Journal of Comparative Economics and a 1998 special issue of China Economic Review.

[4] See Yang (1996), Chang and Wen (1997), Lin and Yang (2000), Kung and Lin (2003), and surveys of the literature on excess mortality by Johnson (1998), Lin and Yang (1998), and Riskin (1998). There is a consensus that the production shortfall alone was not enough to account for the heavy death toll. Other causes of the famine identified by researchers include urban bias in food distribution, excessive grain procurement, wasteful use of food supplies through communal kitchens, grain exports during the early years of the crisis, and radical policies implemented by provincial leaders.

[5] Lin’s hypothesis is consistent with the empirical finding that the total factor productivity in Chinese agriculture fell during the GLF period and remained low until the decollectivization in the late 1970s (Wen 1993).

[6] To the government, this premise appeared to have passed field tests. Between 1953 and 1957, the growth of China’s agricultural production coincided with the collectivization movement. The premise seemed to have been resoundingly reaffirmed when thousands of local cadres outdid one another in making wild claims about grain yields in 1958, the first year of the GLF.

[7] See Lin (1990) and Yang (1996) for detailed descriptions of the collectivization process.

[8] By the fall of 1956, official estimates were that some 20 percent of all members sought to withdraw from cooperatives (Yang 1996).

[9] The 1959 revision was reported in the New York Times on August 27, 1959. The last revision was published in the 1980 edition of the China Statistical Yearbook.

[10] Simultaneously, the government mobilized massive investment funds by raising the rate of accumulation from 24.9 percent of national income (or net material product) in 1957 to 43.8 percent in 1959. Capital investment was concentrated in heavy industries (Riskin 1987, 142).

[11] Constructed using mud and brick, the furnaces burned wood and coal as fuel and used scrub metal as raw materials. They produced iron blocks, which, by the government’s own admission, could meet only “rural requirements.” Yet these iron outputs were proudly included in national statistics. National iron and steel production more than tripled between 1957 and 1960 and then collapsed to its pre-GLF level in 1962.

[12] During an interview conducted by one of the authors in 1999, a formal commune cadre in Henan Province described 1958 as “a year of bumper crops without a bumper harvest.” See also Becker’s (1996) accounts.

[13] In Guangshan County, Henan Province, “cadres reported a harvest of 239,280 tons when it was really only 88,392 tons, and fixed the grain levy at 75,500 tons. When [peasants] were unable to collect more than 62,500 tons, close to the entire harvest, the local cadres launched a brutal ‘anti-hiding campaign’” (Becker 1996, 113).

[14] The aggregate statistics also masked regional variations in procurement policy and the severity of food shortages. For example, Becker (1996) describes in detail Henan and Anhui Provinces’ more radical GLF policies and the resulting famine.

[15] In comparison, according to the Harris-Benedict formula popularized by weight loss programs in the United States (see, e.g., http://www.bmi-calculator.net/bmr-calculator/ harris-benedict-equation/), 2,587 calories of food energy are required to maintain body weight for a 25-year-old man who is 55 kg in weight and 170 centimeters in height and who exercises vigorously everyday.

[16] However, the changes did not come smoothly. In the summer of 1959, at the Lushan Plenum of the Communist Party, Defense Minister Peng Dehuai openly criticized the GLF policies. Enraged, Mao launched a counterattack, deposed Peng and his supporters, and temporarily reinvigorated the GLF.

[17] We do not include other inputs (such as land and farm capital) here, not because they are not important, but because we want to highlight the role of nutrition and resource diversion in as simple a model as possible. For empirical analysis, we shall include all conventional inputs in agricultural production in the specification.

[18] The work capacity of a laborer is related to his or her anthropometric measurements— in particular, height and weight. For example, the body mass index, defined as weight divided by height squared (see Dasgupta 1993; Strauss and Thomas 1995), is frequently used to measure a person’s nutritional status, which affects physical work capacity.

[19] More generally, each crop cycle can be divided into two stages (e.g., Behrman, Foster, and Rosenzweig 1997): a planting stage (usually in the spring) and a harvesting stage (usually in the fall). While food is normally plentiful during the harvesting stage, the supply of food during the planting stage depends on how much grain from the last harvest was saved. Here, we implicitly assume that the beginning of each time period or year in the model matches the planting stage of the crop cycle.

[20] In China, each industrial worker (and each member of his immediate family) was entitled to receive a predetermined amount of food coupons from the government. The amount of food entitlement varied with job types. For example, in 1956, the national average of monthly rations of grain for laborers assigned to the most physically demanding jobs was 25 kg; for hard laborers, 20 kg; for light laborers, 16 kg; and for white-collar employees, 14 kg (Cheng 1982, 206). Retail prices of staple food and industrial wages were both set by the government to ensure the affordability of the rationed food. Prices were not market clearing and played little role in resource allocation.

[21] The Euler equation can be derived using either the recursive method (Stokey, Lucas, and Prescott 1989) or the Lagrange method (Chow 1997).

[22] This is a simplification. The history was more complicated (see n. 16). If we simulate a delay by one year of the policy reversal, the collapse of output would be even deeper and last longer.

[23] The government also publishes an official weather variable that measures the percentage of sown acreage experiencing 30 percent or more reduction in yield due to flood, drought, frost, or hail. However, there is reason not to use this variable. Given the party line explanation of the GLF disaster, it is plausible that crop failures caused by other factors, such as the GLF policies, may have been attributed to bad weather. Nevertheless, we shall examine whether our empirical findings are sensitive to the choice of weather variables.

[24] After the GLF, while the government altered its policies, it did not loosen the grip of central planning in agriculture until 1978.

[25] Since weather quality is classified into five categories, there are 25 possible categories of weather conditions (or 25 weather dummies) for any two years under consideration.

[26] We obtain similar results when weather effects are removed from the analysis.

[27] In fact, as aggregation reduces the cross-sectional variation in food availability but not the negative effect of malnutrition, it is plausible that the aggregate estimate of the food elasticity is higher than household estimates.

[28] The period average mortality rates for the three provinces are 43.5, 31.1, and 26.4 per thousand, respectively. These rates are much higher than both the pre-GLF mortality rates of 11.3, 11.7, and 8.2 per thousand recorded in the three provinces and the national average mortality rate of 17.3 for the GLF period (Lin and Yang 1998).

[29] The lowest provincial average grain output was reached in 1961 (see table 2).

{1} 1 ^p very good, 3 ^p average, and 5 ^p very bad.